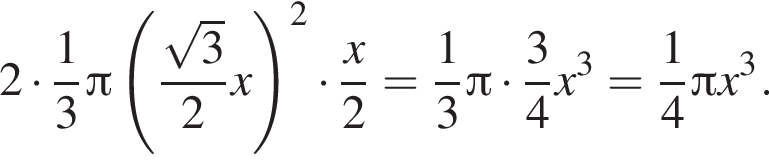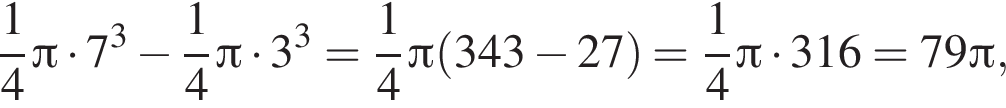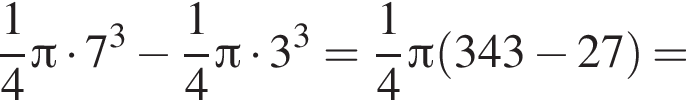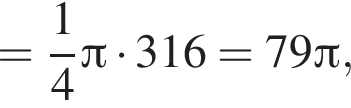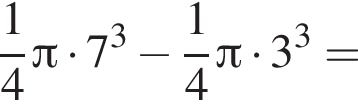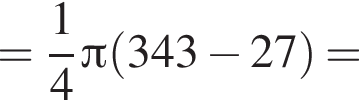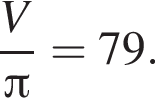На рисунке изображены две окружности с центрами в точках A и B. Если MK = 48, то сумма радиусов этих двух окружностей равна:
Централизованное тестирование по математике, 2022
Определите координату точки А, изображенной на координатной прямой.
Найдите значение выражения 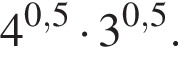
Даны пары значений переменных x и y: 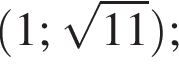
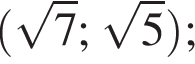

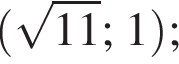
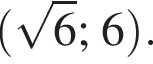 Укажите пару, которая НЕ является решением уравнения
Укажите пару, которая НЕ является решением уравнения 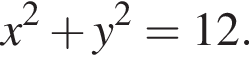
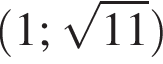

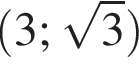
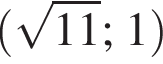
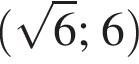
Функция y = f(x) задана на промежутке 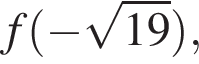
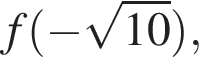
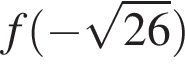 в порядке убывания.
в порядке убывания.
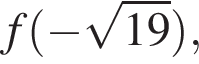


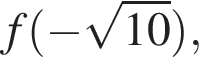
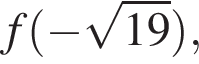
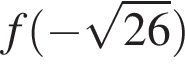

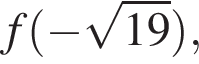


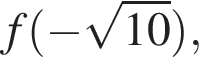

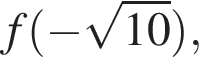


Показ фильма начался в 17 часов 27 минут, а закончился в 19 часов 12 минут. Какова (в часах) продолжительность показа фильма?
Ширина участка Иванова равна 72 м, а длина — 96 м. Участок Петрова имеет ширину на 27 м меньше, чем ширина участка Иванова. Чему равна длина участка Петрова (в метрах), если отношение ширины к длине у обоих участков одинаково?
Из точки A к окружности с центром O проведены две касательные AB и AC, где B и C — точки касания. Через точки C и O проведена прямая, которая пересекает касательную AB в точке M (см. рис.). Найдите градусную меру угла 1, если ∠AMC = 44°.
Найдите значение выражения 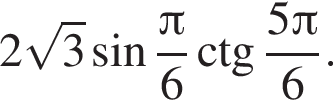
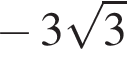
Укажите номер пары взаимно простых чисел.
Упростите выражение  если
если ![]() и
и ![]()

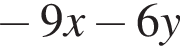
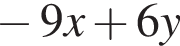

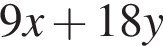
Укажите номера функций, областью определения которых является множество всех действительных чисел.
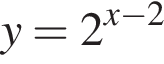
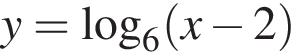


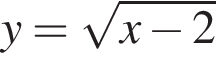
Даны две параллельные плоскости α и β, расстояние между которыми равно ![]() Прямая а пересекает плоскости α и β в точках А и В соответственно и образует с ними угол 30°. Найдите длину отрезка АВ.
Прямая а пересекает плоскости α и β в точках А и В соответственно и образует с ними угол 30°. Найдите длину отрезка АВ.
Дана функция 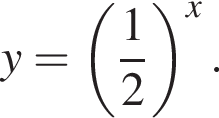 График функции y = g(x) получен из графика функции
График функции y = g(x) получен из графика функции 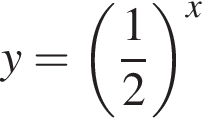 сдвигом его вдоль оси абсцисс на 1 единицу влево и вдоль оси ординат на 3 единицы вниз. Значение g(−4) равно:
сдвигом его вдоль оси абсцисс на 1 единицу влево и вдоль оси ординат на 3 единицы вниз. Значение g(−4) равно:
Наибольшим целым решением совокупности неравенств 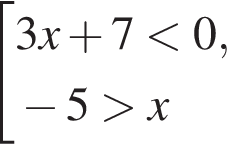 является:
является:
Для неравенства 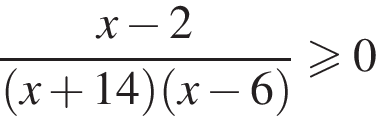 укажите номера верных утверждений:
укажите номера верных утверждений:
1) неравенство верно при 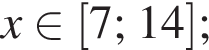
2) количество всех целых решений неравенства равно 21;
3) наименьшее целое решение неравенство равно −13;
4) неравенство равносильно неравенству 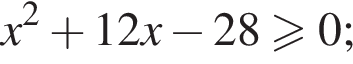
5) число 3 является решением неравенства.
Тангенс угла наклона к оси абсцисс касательной, проведенной к графику функции 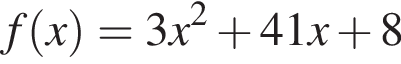 в точке с абсциссой x0, равен −7. Найдите значение x0.
в точке с абсциссой x0, равен −7. Найдите значение x0.
Найдите объем прямой призмы ABCDA1B1C1D1, в основании которой лежит параллелограмм ABCD, если длины ребер AB и AA1 равны 4 и 1 соответственно, а расстояние точки A1 до прямой CD равно 5.
На координатной плоскости дана точка A(5; 3). Для начала каждого из предложений А−В подберите его окончание 1–6 так, чтобы получилось верное утверждение.
A) Если точка В симметрична точке А относительно оси ординат, то расстояние между точками А и В равно ...
Б) Если точка С симметрична точке А относительно прямой у = 1, то расстояние между точками А и С равно ...
B) Если точка N симметрична точке А относительно точки D(3; −1), то расстояние между точками А и N равно ...
1) 8
2) 10
3) 4
4) ![]()
5) ![]()
6) ![]()
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
В прямоугольном треугольнике ABC ∠C = 90°, CH — высота, проведенная к гипотенузе, 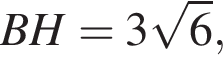 ∠BCH = 30°. Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
∠BCH = 30°. Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
A) Длина стороны ВС треугольника АВС равна ...
Б) Длина стороны АС треугольника АВС равна ...
B) Расстояние от точки пересечения биссектрис треугольника ABC
до стороны AB равно ...
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) 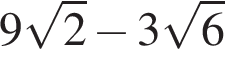
6) ![]()
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Дана треугольная пирамида SABC. Точки К и N являются серединами ребер SA и АС соответственно, точка М лежит на прямой SB (см. рис.). Выберите три верных утверждения.
1. Прямая KN параллельна плоскости BSC.
2. Прямая NM пересекает плоскость BSC.
3. Прямая КМ пересекает прямую ВС.
4. Прямая КМ лежит в плоскости ASВ.
5. Прямая NM пересекает прямую ВС.
6. Прямая KN пересекает плоскость BSC.
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 135.
Пол на кухне начали выкладывать квадратной плиткой так, как показано на рисунке. Размеры плитки 30 см × 30 см. Размеры кухни указаны на рисунке в метрах. Какое наименьшее количество плиток может понадобиться, чтобы выложить весь пол? Толщиной шва пренебречь.
Пусть 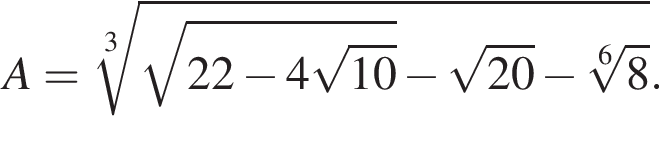 Найдите значение выражения A12.
Найдите значение выражения A12.
Найдите (в градусах) корень уравнения  на промежутке (0°; 45°).
на промежутке (0°; 45°).
Дан параллелограмм ABCD, 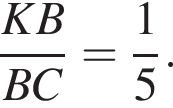 Отрезок DK пересекает сторону АВ в
Отрезок DK пересекает сторону АВ в
Найдите сумму квадратов корней уравнения 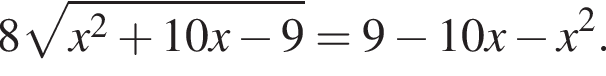
Найдите произведение наименьшего целого решения на количество всех целых решений неравенства
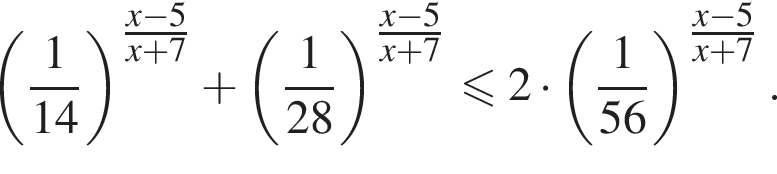
При делении натурального числа b на 25 с остатком, отличным от нуля, неполное частное равно 9. К числу b слева приписали некоторое натуральное число а. Полученное натуральное число разделили на 20 и получили 18 в остатке. Найдите число b.
В параллелограмме длина одной из сторон вдвое больше длины другой, а острый угол равен 60°. Большая сторона параллелограмма лежит в плоскости α, а его большая диагональ образует с этой плоскостью угол, синус которого равен ![]() Найдите значение выражения
Найдите значение выражения ![]() где β — угол между плоскостью параллелограмма и плоскостью α.
где β — угол между плоскостью параллелограмма и плоскостью α.
Найдите сумму квадратов корней (квадрат корня, если он единственный) уравнения
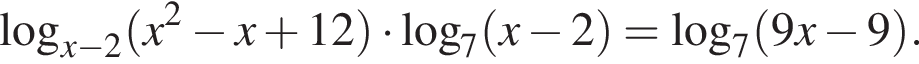
Отрезок BD является биссектрисой треугольника АВС, в котором 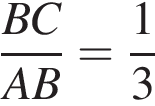 и
и 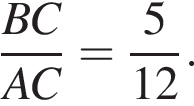 По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 14 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?
По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 14 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?
Равнобедренная трапеция с основаниями длиной 7 и 3 и острым углом 60° вращается вокруг прямой, содержащей ее боковую сторону. Найдите объем тела вращения V и в ответ запишите значение выражения ![]()


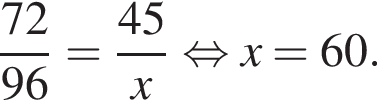
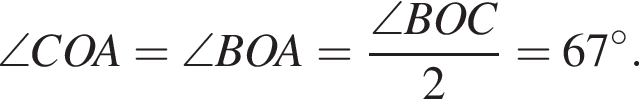
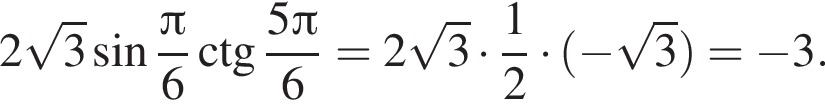
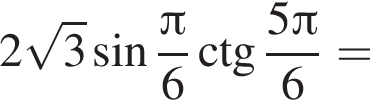
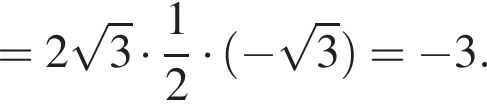
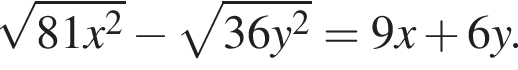
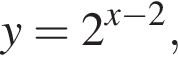
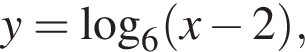
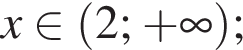
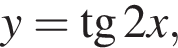
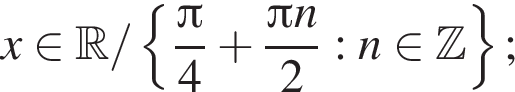

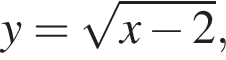
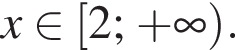
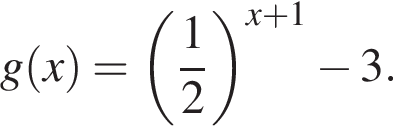 Тогда
Тогда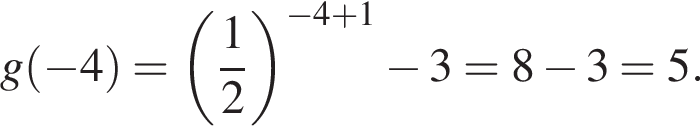
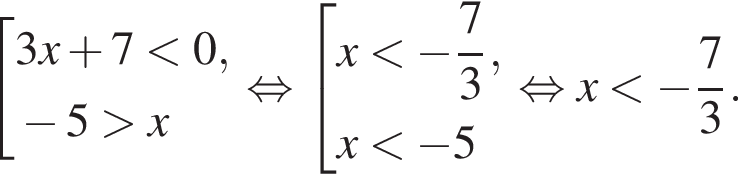
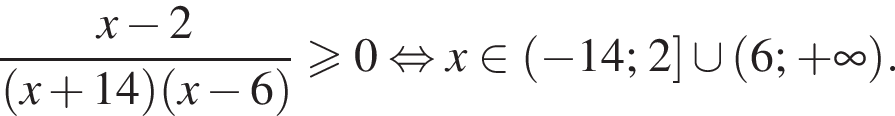
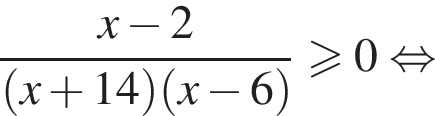
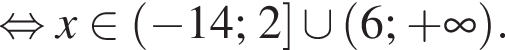
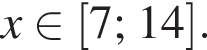
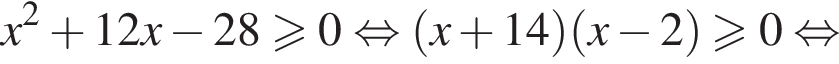
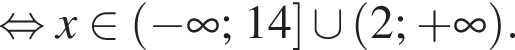
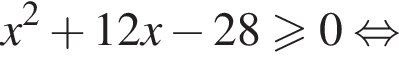
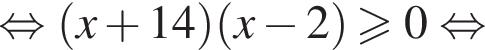
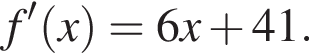
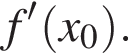 Следовательно, имеем:
Следовательно, имеем: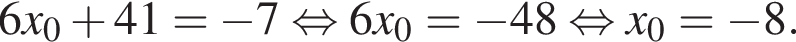
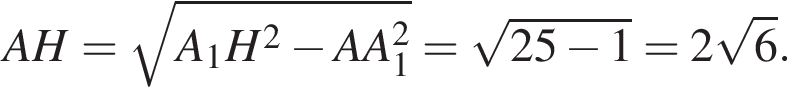
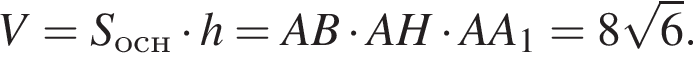
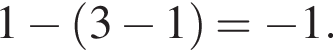 Тогда
Тогда 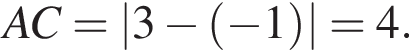
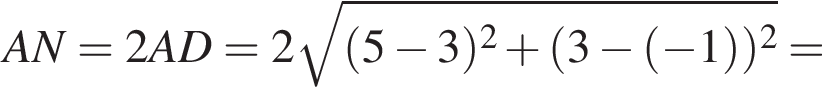
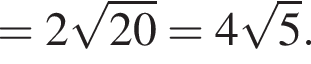
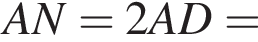
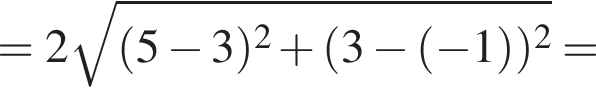
 и
и  Из прямоугольного треугольника CBA получаем
Из прямоугольного треугольника CBA получаем  и
и 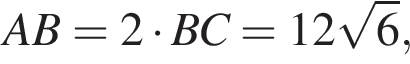 следовательно,
следовательно, 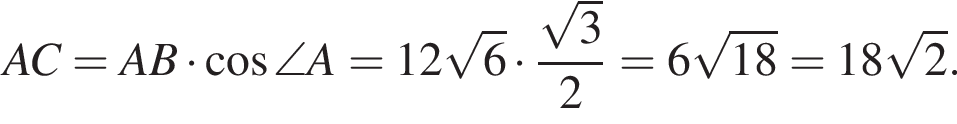
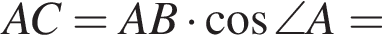
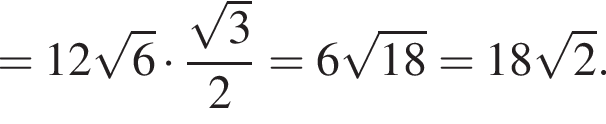
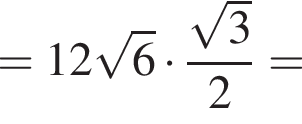
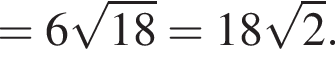
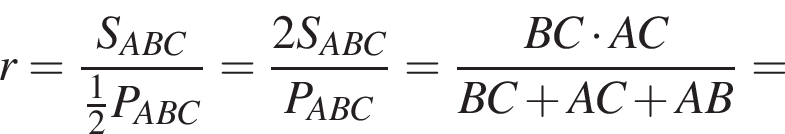
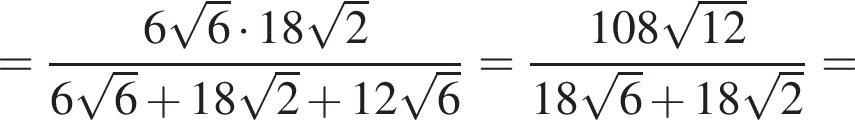
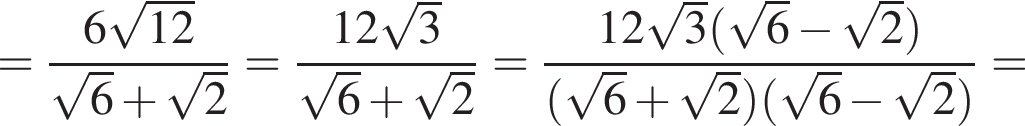
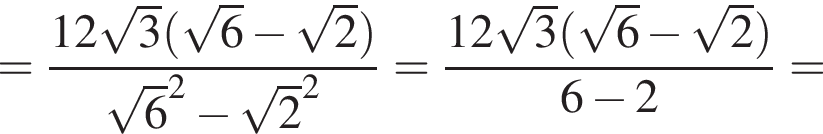
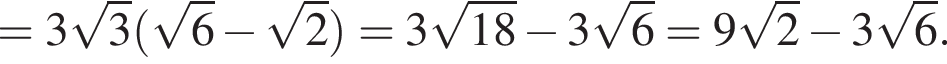
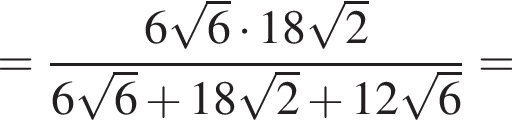
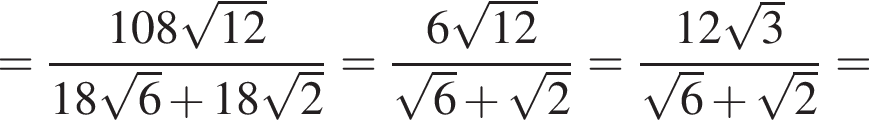
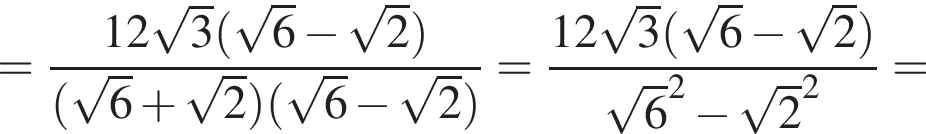
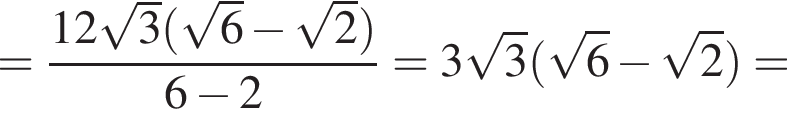
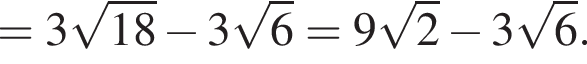
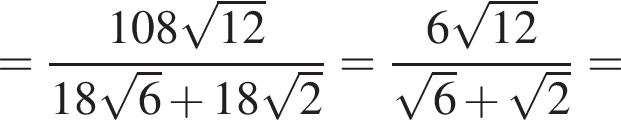
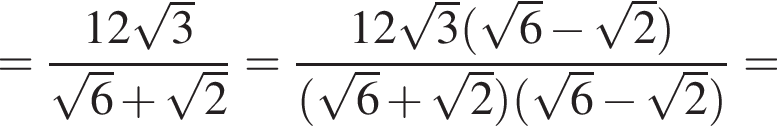

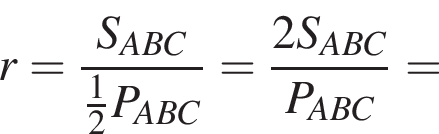
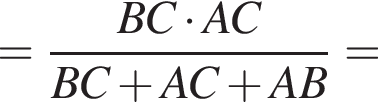
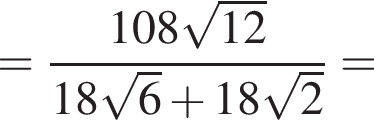
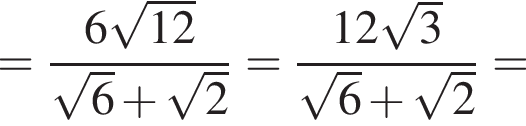
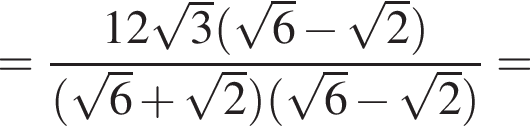
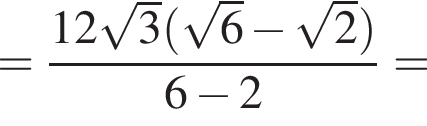
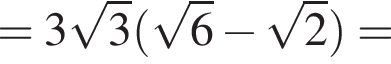
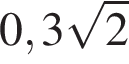 м.
м. При этом 14 плиток нужно будет аккуратно разрезать по диагонали и уложить вдоль стен, а остальные 82 уложить целыми.
При этом 14 плиток нужно будет аккуратно разрезать по диагонали и уложить вдоль стен, а остальные 82 уложить целыми.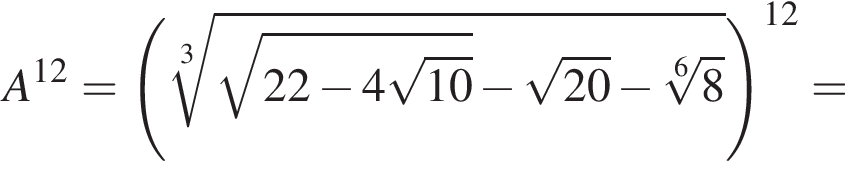
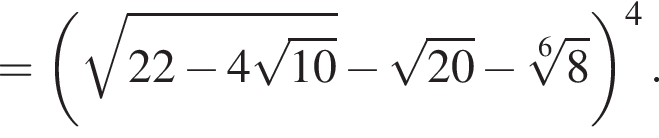
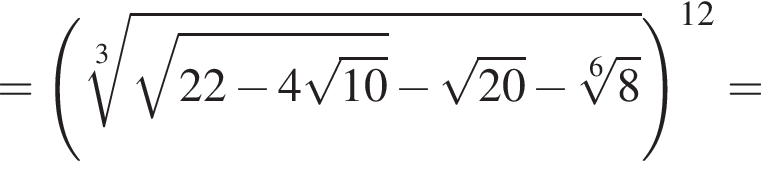
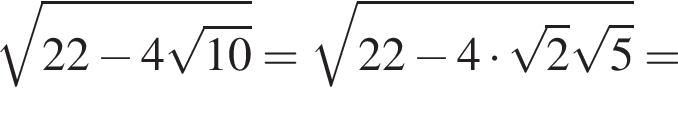
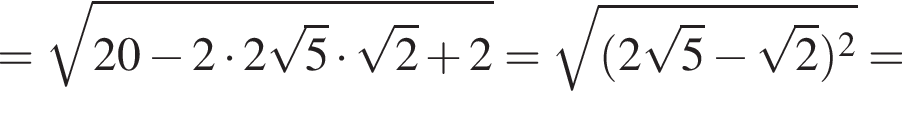
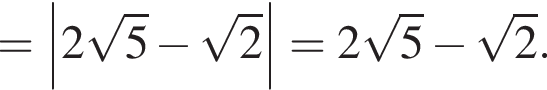
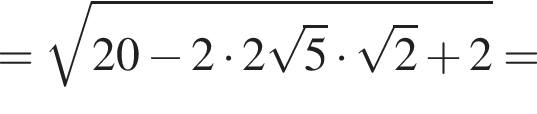
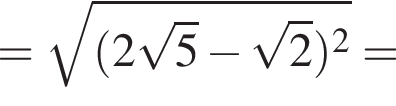
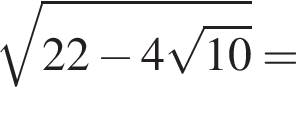
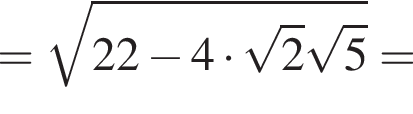
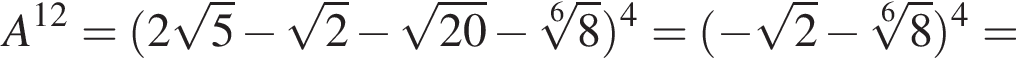
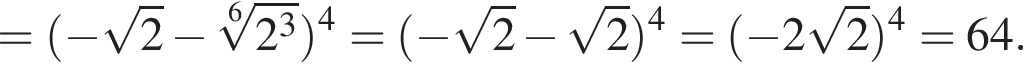
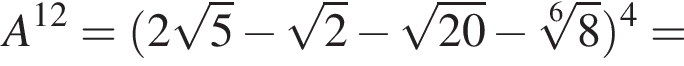
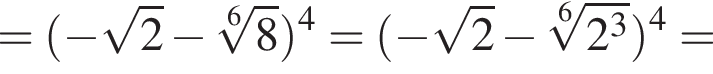
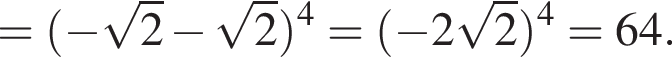
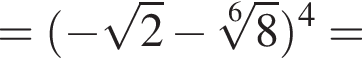
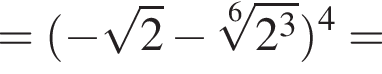
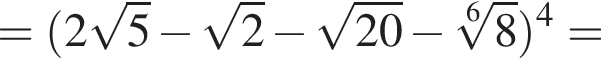
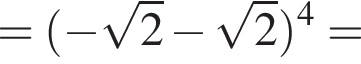
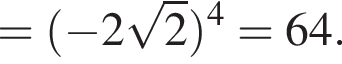
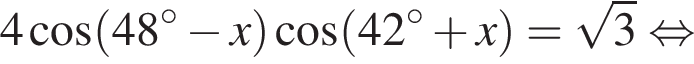


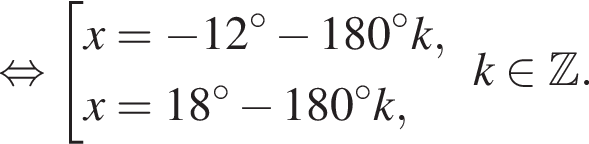
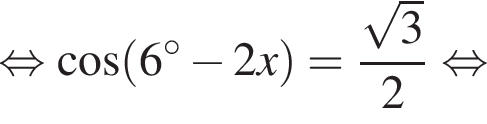
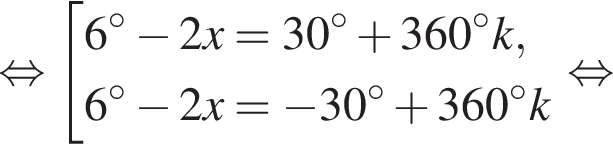

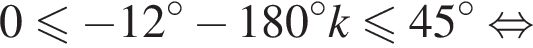
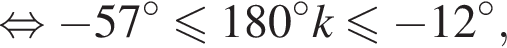
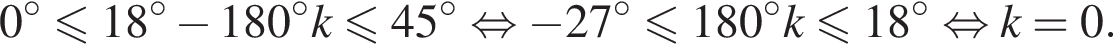
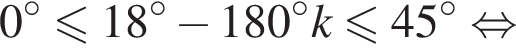
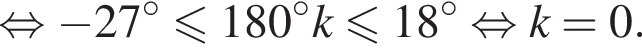
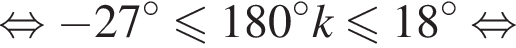
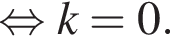
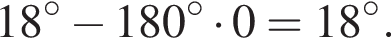
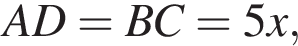 тогда
тогда  и
и 
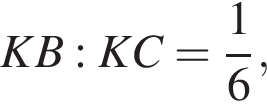 поэтому
поэтому 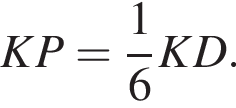
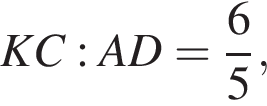 поэтому
поэтому 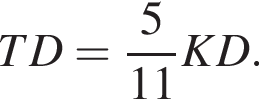
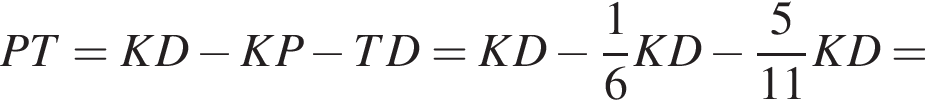
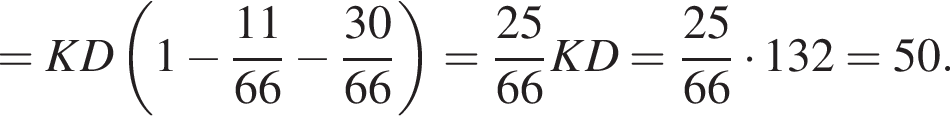
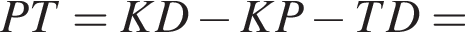
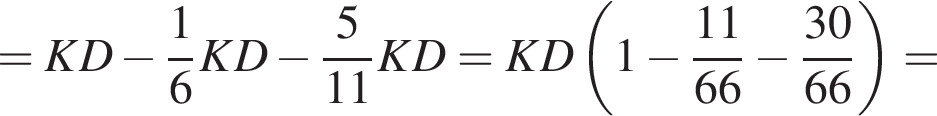
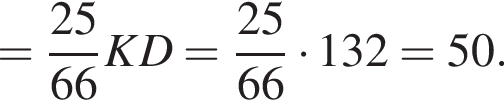
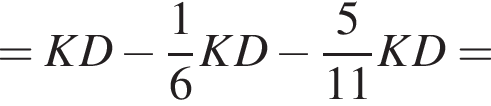
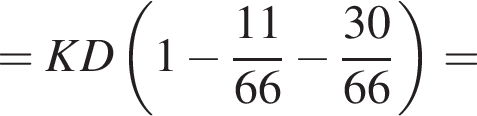
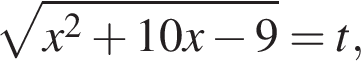 тогда
тогда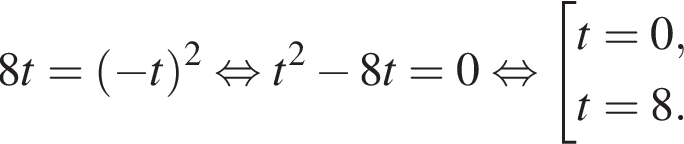
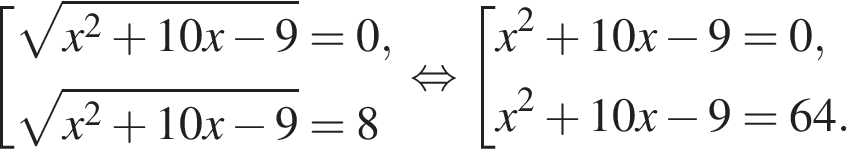
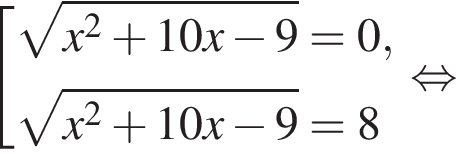
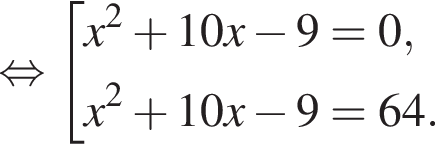
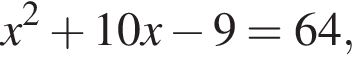 то
то 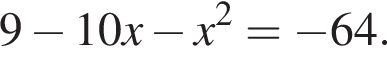 Подставив полученные числа в исходное уравнение, получим:
Подставив полученные числа в исходное уравнение, получим: 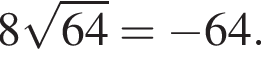 Следовательно, корни второго уравнения не являются решением. Решим первое уравнение и получим два решения:
Следовательно, корни второго уравнения не являются решением. Решим первое уравнение и получим два решения: 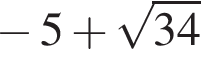 и
и 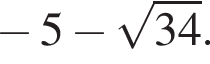
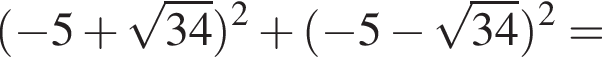
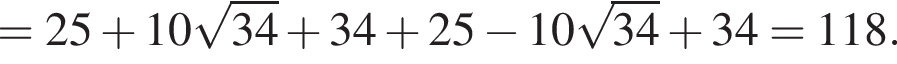
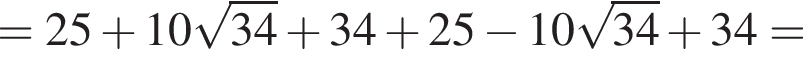
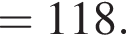
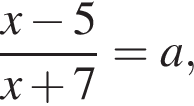 тогда
тогда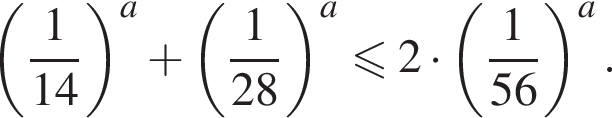
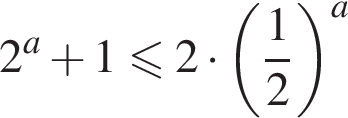
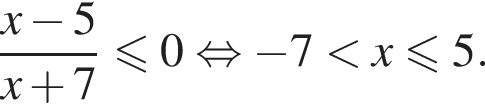
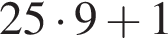 до
до 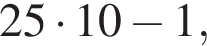 то есть от 226 до 249 (для 225 не было бы остатка, а для 250 частное было бы равно 10).
то есть от 226 до 249 (для 225 не было бы остатка, а для 250 частное было бы равно 10). 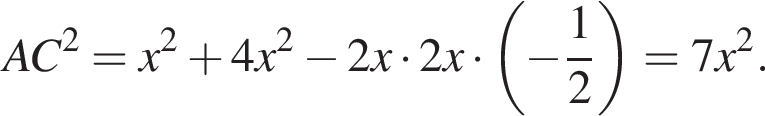
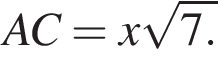 Пусть h — расстояние от прямой BC до плоскости α. Тогда
Пусть h — расстояние от прямой BC до плоскости α. Тогда 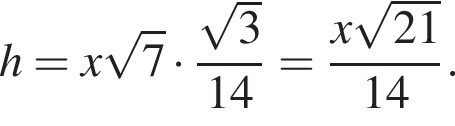
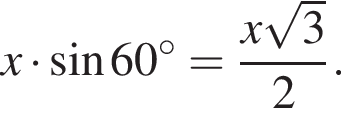 Тогда
Тогда 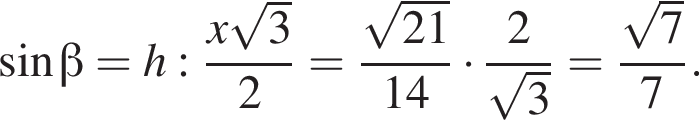
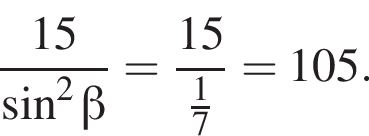
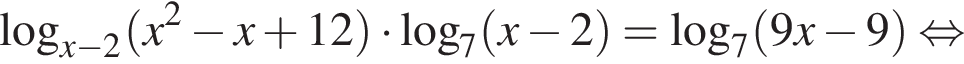
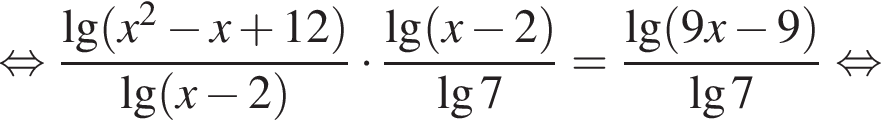
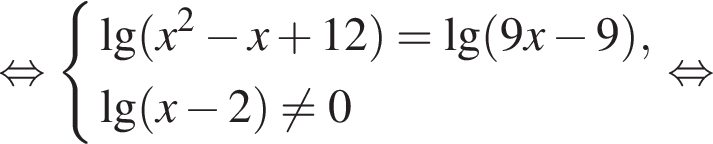
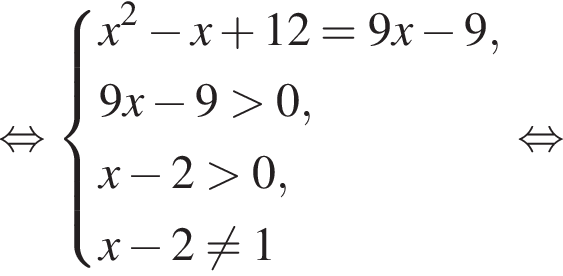
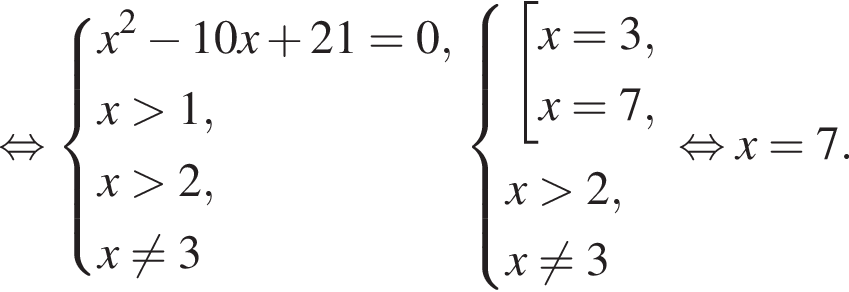
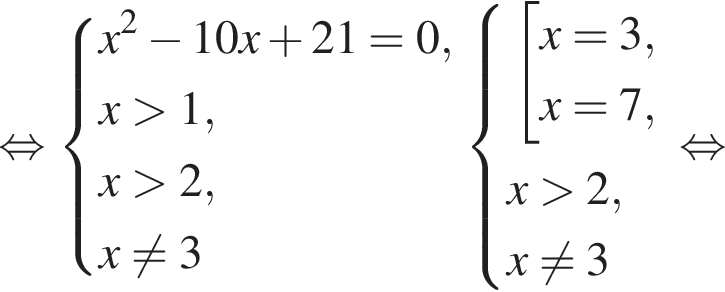

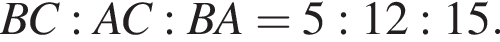 По свойству биссектрисы получаем, что
По свойству биссектрисы получаем, что 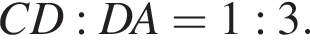 Значит, если
Значит, если  то
то 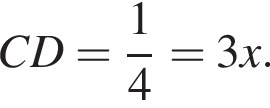
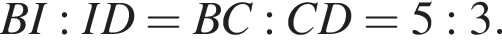 Значит, можно считать, что скорость первого тела равна 5υ, а второго 3υ. Время движения обратно пропорционально скорости, из условия следует, что
Значит, можно считать, что скорость первого тела равна 5υ, а второго 3υ. Время движения обратно пропорционально скорости, из условия следует, что 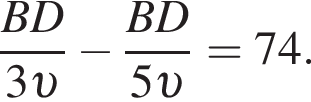
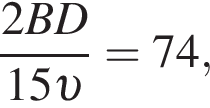 откуда
откуда 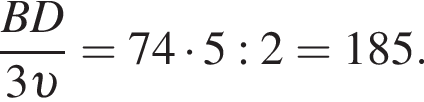
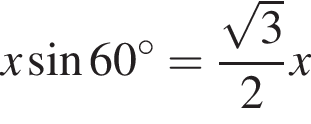 и потому объем двух таких конусов равен
и потому объем двух таких конусов равен